Expert Series: The Advantages of Chirp Technology

Chirps are great for low power wide area networks (LPWAN) because they occupy a single dimension.

Let’s start with a real-world analogy: it is difficult to get lost in a one-dimensional space. For instance, if you walk along a coastline or a river it is fairly easy to find your way back. Similarly, it is possible to set up an appointment with a friend in a one-dimensional space (in a loose manner) such as “Let’s meet on Main Street near the restaurants.” If you’re both walking along Main Street near the restaurants at roughly same time, you will very likely encounter one another.

It is much more difficult to do the same thing in two dimensions. For instance, if you wish to pick mushrooms in a forest with a friend, you would need to meet in the morning at a known place and time before you start wandering.

Long range, low power wireless technologies work in much the same way. These technologies have receivers to detect signals at a low level, a level often below the noise floor. Additionally, detection and synchronization must be performed at the same time, which means answering the following three questions:

• Is there a signal?
• What is the exact frequency of the signal?
• What is the start time of the signal?

Detecting and synchronizing such a low level signal is like looking for a needle in a haystack.

As a result, without assistance data, GPS receivers can take several minutes to detect satellites. This is due to the fact that, before it can detect the presence of a satellite signal, the receiver has to guess the satellite’s exact frequency error, which comes from the Doppler frequency shift. The receiver must also guess the correct timing of the satellite’s broadcast stream (its code phase). This is a search in two dimensions. The only way this type of search can be successful is to try all combinations of frequency offset and timing offset. Since it is not possible to test all combinations in parallel, it can take a long time to get a fix. Any Direct Sequence Spread Spectrum (DSSS)-based LPWAN system will suffer from the same detection complexity.

Let’s look at another example: Ultra Narrow Band systems. In such systems, the frequency error of the transmitting devices is much higher than the modulation bandwidth. As a consequence, there is no concept of “channels”, and the frequency of the signal to be detected is a purely random variable. To ensure that the gateway doesn’t miss any signals, it must implement many receivers in parallel. So, if the modulation bandwidth is 100Hz the gateway would need one receiver every 100Hz, or even every 50Hz. Each of these receivers, then, needs to implement a time correlator to detect the signal. This is also a two-dimensional search.

When we designed LoRa®, we knew that a simple receiver was key, and we came upon chirps. When it comes to detection, chirps have a very interesting property: they have a time/frequency equivalence. This means that a frequency offset is similar to a time offset. In more mathematical terms, for any frequency offset, there exists a time offset which cancels it. It is possible to mathematically prove that, among constant envelope modulations, only linear chirps have this property. The time/frequency equivalence is illustrated in the figure below. Note, several combinations (of frequency offset and timing offset) give the same final offset between the signal desired and the prototype signal used for correlation.

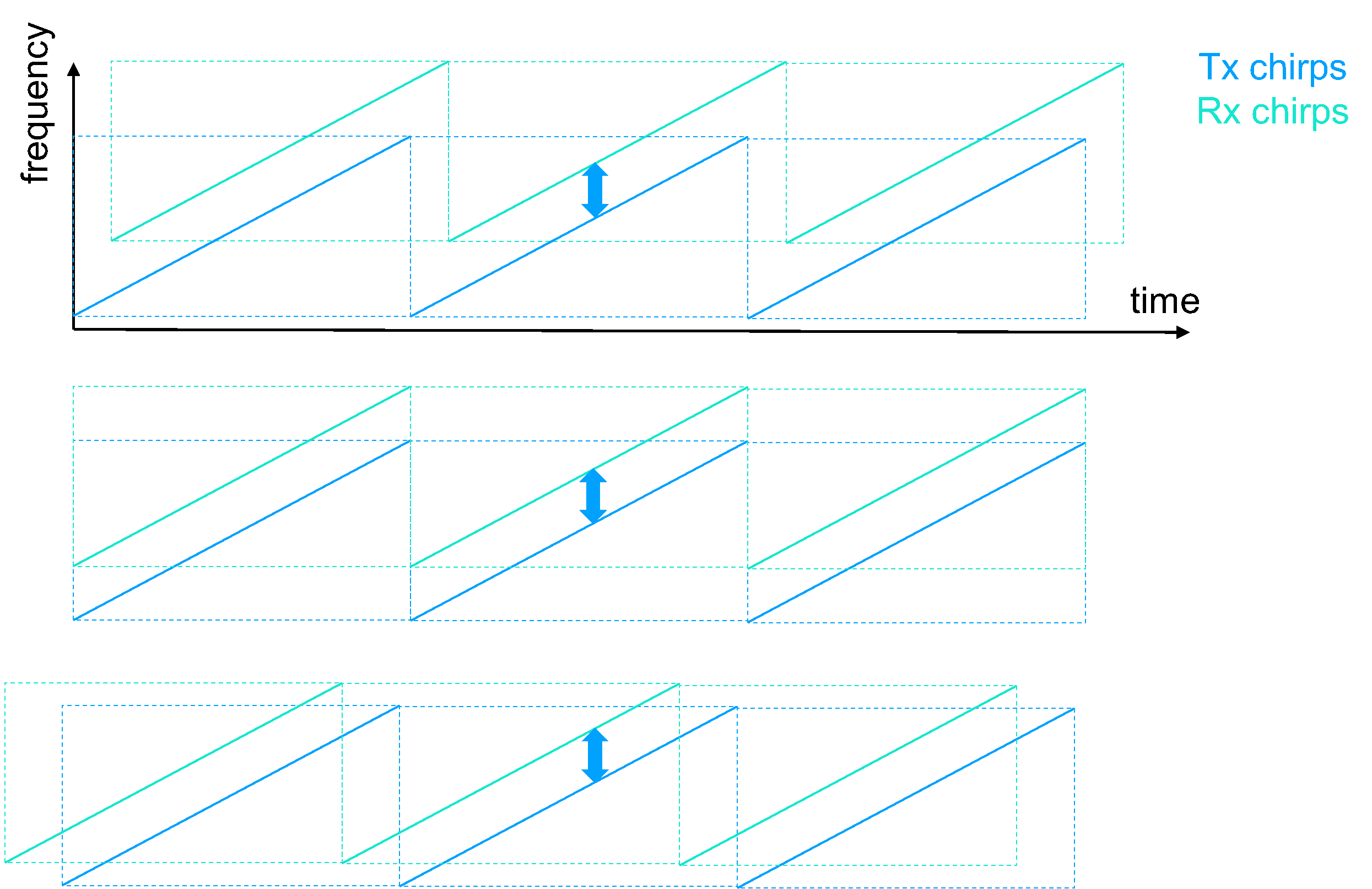
Figure 1: Chirp Frequency/Time Offset Equivalence

Since the offset is the same for different combinations, we don’t have to call it either a “frequency offset” or a “timing offset”; the desired offset is a single dimension.

The consequence of the time/frequency equivalence is that chirp detection does not require accurate time and frequency synchronization. We can detect a signal without having to guess its precise frequency first. With respect to LoRa, a LoRa-based receiver will first detect a signal and then synchronize it precisely, using the dedicated symbols of the preamble.

So, instead of searching in two dimensions, we first search in one dimension and then in another. This significantly decreases the complexity of the search. For example, with SF12, LoRa has 2*4096 timing possibilities, and even more frequency possibilities, just like any long-range modulation with the same sensitivity. To simplify this example, imagine that each dimension has 5000 possibilities. A two-dimension search will have a complexity of 5,000*5,000. In contrast, two successive single dimension searches have a complexity of only 2*5,000. This makes the LoRa receiver 2,500 times simpler.

What you should remember here is that, thanks to the time/frequency equivalence of chirps, the reception of LoRa-based signals is simpler than other long-range technologies because we only have to search in one dimension rather than two. This explains why LoRa uses downlinks and why Semtech can offer affordable gateway solutions.

LoRa® is a registered trademark or service mark of Semtech Corporation or its affiliates.